Compactness

Pancakes, anyone?

Open sets are not pancakes.

Consider the open disk containing all x and y coordinates such that x squared plus y squared is less than 1. That open disk, is, unfortunately, not a pancake.

There are many reasons open sets are not pancakes. One is that pancakes are yummy.

But it’s helpful to imagine covering someone with pancakes…	…when what you’re actually doing is covering a space with open sets.
	For example, we may cover the x-y plane with a bunch of open disks.

So, in this chapter, I conflate “pancakes” and “open sets.”

When you see a reference to “pancakes”, feel free to mentally cross it out and replace it with “open sets,” and vice versa, depending on your preference.

How many ways can you cover someone with pancakes?

Given a particular friend…

…there are lots of ways to completely cover them with pancakes.

You could cover them with one pancake.

Or you could cover them with two pancakes — one covering each half of their body.

Or you could cover them with one pancake, and then pile many more pancakes on top of that one.

Similarly, given a set in space…

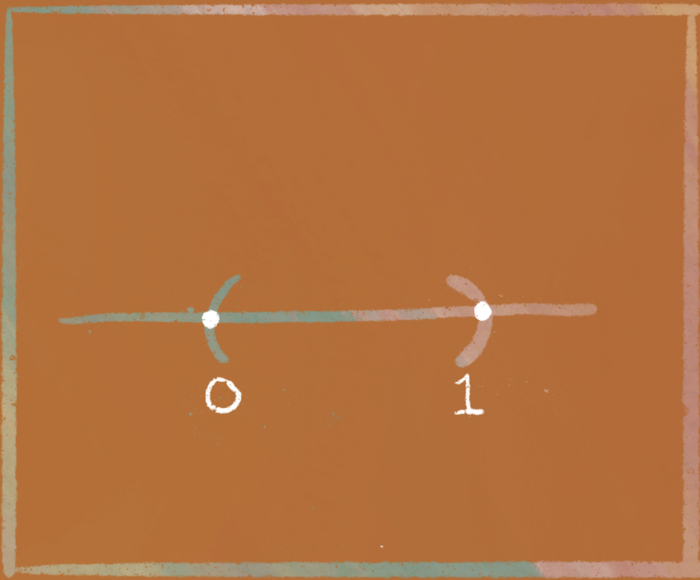
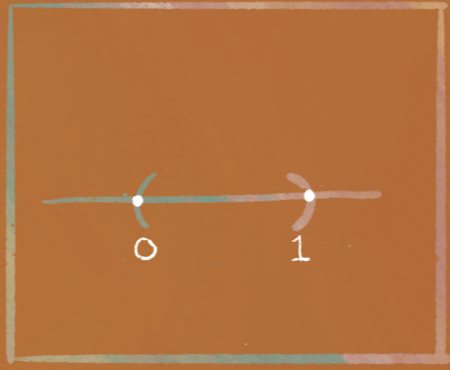
…there are a lot of ways to completely cover it with open sets. For example, $(0,1)$ could be covered by….

One pancake.	One bigger pancake.	Two overlapping pancakes.	Or, infinitely many overlapping pancakes. Or, more formally…
The open interval $(0,1)$	The open interval $(-1,2)$	The open interval $(-1,\frac{3}{4})$ and $(\frac{1}{4},2)$	The infinite collection of open intervals $\{(\frac{1}{n},1): n \in \mathbb{N}\}$

So, what exactly is a cover?

Let’s say a “cover” of your friend …	…is a collection of pancakes…	…that covers every inch of them.

And let’s say a “cover” of a set $S$…	…is a collection of open sets…	…that completely contains $S$.

Formally, a $\textit{cover}$ of $S$ is a collection $\mathcal{C}$ of open sets $U$ such that:

$$ S \subseteq \bigcup\limits_{U \in \mathcal{C}} U.$$

In other words, a cover $\mathcal{C}$ of the set $S$ is a collection of open sets $U$ (pancakes) such that if you take the union of all the open sets in the collection $\mathcal{C}$, it contains the set $S$.

How many pancakes did we use?

Pancakes don’t grow on trees.

So ideally, we only use a finite number of pancakes.

Note that some covers use finitely many pancakes.

And some covers use infinitely many.

So, when I say a cover is finite, I mean the cover uses finitely many pancakes.

Formally, when I say that $\mathcal{C}$ is a finite cover, I mean that there are only finitely many open sets in $\mathcal{C}$. Of course, each of these open sets could contain infinitely many points.

Did you need all of those pancakes?

Sometimes, we used more pancakes than we needed to completely cover a person.

So once you have a cover…

…you might want to eat the pancakes you didn’t need. A subcover is any subcollection of those pancakes that still covers your friend.

If it doesn’t completely cover your friend, it isn’t a subcover.	And if it requires adding new pancakes that weren’t in the original cover, it isn’t a subcover either.
That is, your friend might resent that you have exposed them to the elements by removing the pancakes that had been keeping them covered.	And they also might resent you for adding in more pancakes when they already had enough covering them.

Informally, a subcover is a cover …

…. after you’ve eaten some of the pancakes in it.

For example, suppose you want to cover the interval $(-1,1)$ . You can cover it with $\set{(-1,1),(-1/2,1/2)}$ . And after you’ve munched away on a pancake in that cover, a subcover you’re left with is $\set{(-1,1)}$ .

Formally, a subcover is a subcollection of a cover, that is still a cover.

So if you consider any particular cover…

…when you remove a pancake…

…you might get a subcover of it.	…and you might not.
Two intervals cover up a line in the plane.	(If you get too gluttonous, and leave any part of the set you were trying to cover expose).

How many pancakes can we remove?

Sometimes, you’ll start with an infinite cover…	…and be able to remove enough pancakes to end up with a finite subcover.
	And your friend will breathe a sigh of relief that they no longer bear the weight of unnecessary pancakes.

But other times, you won’t be able to.

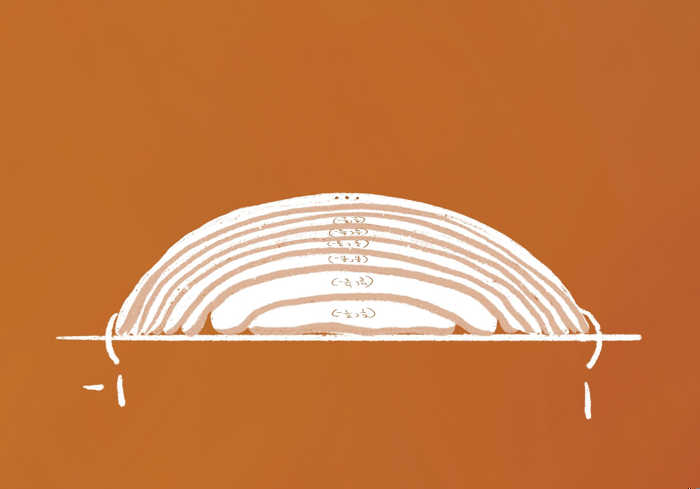
For example, we suppose we want to cover the set $(-1,1)$…

with the following collection…

$$\left\{\left(-\frac{1}{2},\frac{1}{2}\right), \left(-\frac{3}{4},\frac{3}{4}\right), \left(-\frac{4}{5},\frac{4}{5}\right), \cdots \right\}$$

…which we can write succinctly as…

$$\left\{ \left(-\frac{n}{n+1},\frac{n}{n+1} \right) : n \in \mathbb{N}\right\}.$$

There is no way you can take away so many pancakes that you leave a finite number of pancakes there, and it still covers the set $(-1, 1)$.

Informally, this is because when you take any finite subset of the cover, you end up exposing a bit of edge of the set. You’ll prove it formally in the puzzle at the end of this section!

How do we know which covers have spare pancakes?

Ok fine, so we know that when you look at covering $(-1,1)$…

There are some covers …	…that have finite subcovers.
	For example, suppose you are trying to cover the interval (-1,1). The cover {(-1,1),(-1/2,1/2),(-1/3,1/3),…} has a subcover of {(-1,1)}.

But there are other covers ….	that have no finite subcover.
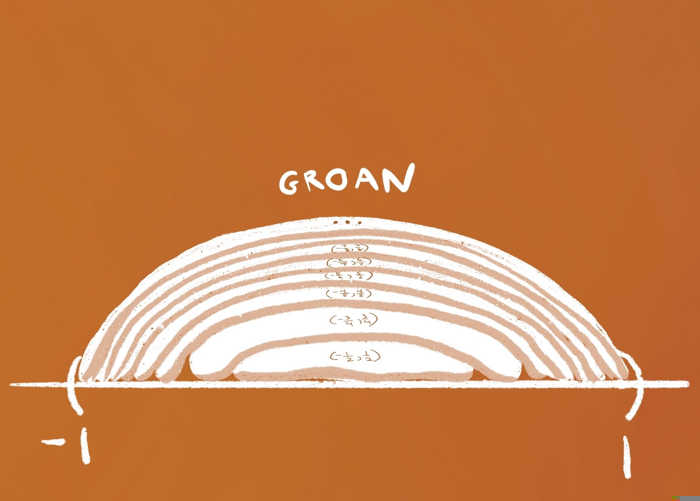	For example, continue supposing you are trying to cover the interval (-1,1). Your set will be left groaning under the unbearable weight. Because the cover {(-1/2,1/2),(-1/3,1/3),(-1/4,1/4)…} has no finite subcover. That is, there is no way to remove pancakes and only leave a finite many, and still cover the set.

So what?

Here’s the big thing: there are some sets, which, given any cover of them, always reduce to a finite subcover. In those sets, any infinite cover will always have spare pancakes to munch on.

For example, look at $[-1,1]$.

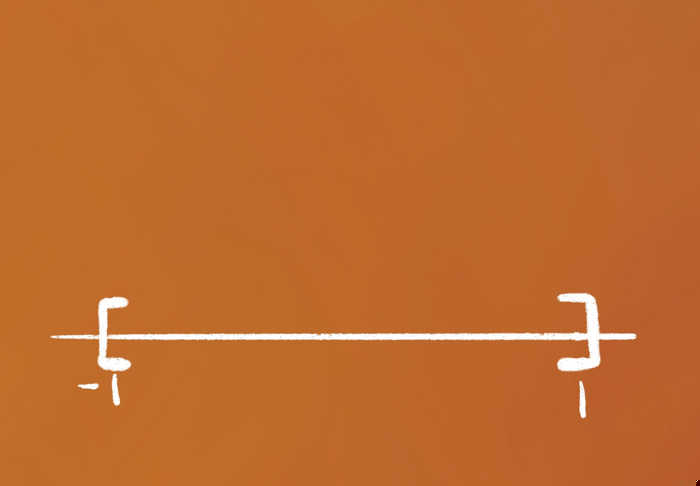
You can cover it the following way…	…and get a finite subcover.
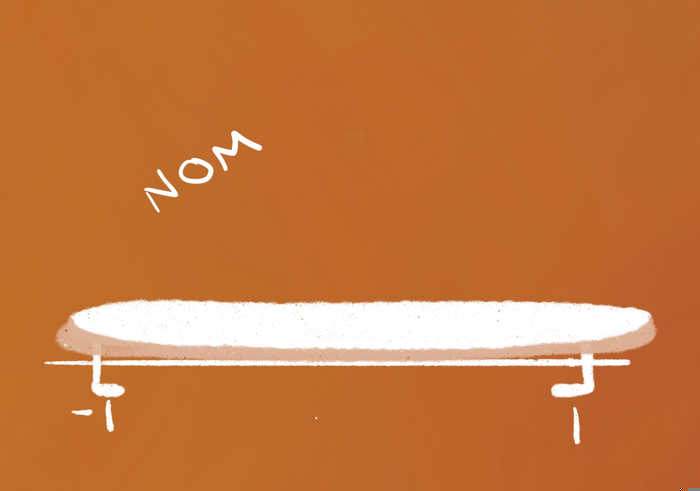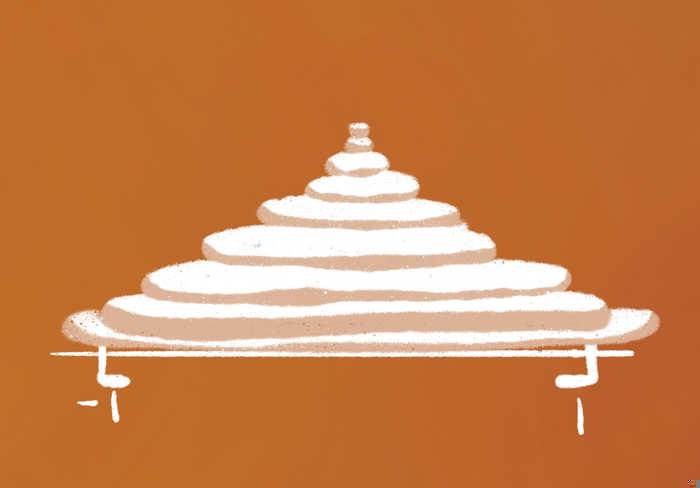
With a pyramid of pancakes, the base of which covers the entire set.	By just eating pancakes at the top (nom nom nom) until you’re left with only one big pancake at the bottom, which is a subcover.

Or you can cover it in the following way…	…and get a finite subcover.
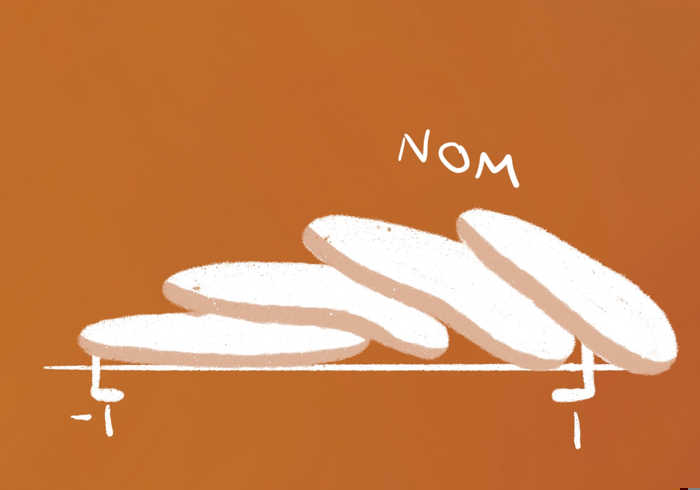With a haphazard collection of pancakes.	By eating all the pancakes you don’t need to cover the set.

And in fact, it turns out, no matter how you cover the interval $[-1,1]$, you can reduce the cover to a finite subcover.

So what’s so great about this set?

It is so low-maintenance!

Given an infinite amount of information about the set’s cover…	…you can always just reduce that…	…to a finite amount of information.

So, let’s call any set like this a “compact set” as a thank-you to the conciseness of the information needed to describe any cover of the set.

Formally, let’s say a set is compact when every single cover of it (no matter how big) has a finite subcover.

So the set $[-1,1]$ is compact.	Because (we’ll prove later) every cover of it has a finite subcover.

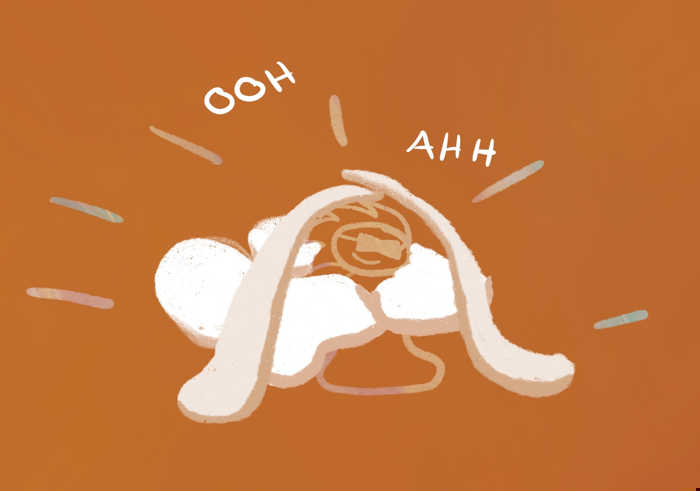
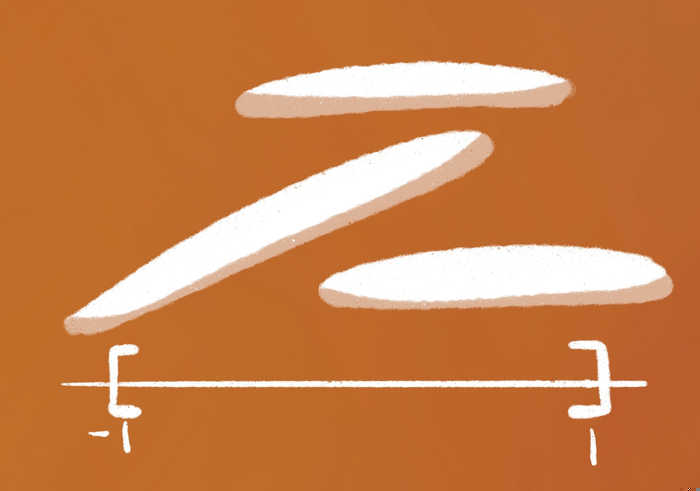
But the set $(-1,1)$ is not compact.	Because there is a cover of it with no finite subcover.
	In particular, the cover {(-1,1),(-1/2,1/2),(-1/3,1/3),…} had no finite subcover.

What’s the point of compact sets?

“Compactness is the next best thing to finiteness,” says Prof. Francis Su.

It’s true. That is, a compact set may not be finite, but it’s the “next best thing” — any open cover of it can be reduced to a finite one.

This ability to reduce a lot of information to just a finite amount means compact sets are much easier to prove things about than other sets.

As a result, compact sets play a big role in differentiation and integration, as we’ll see later.

Puzzle

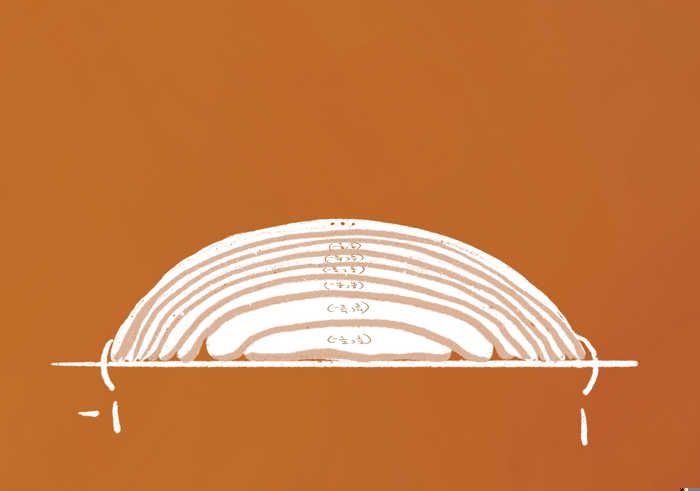
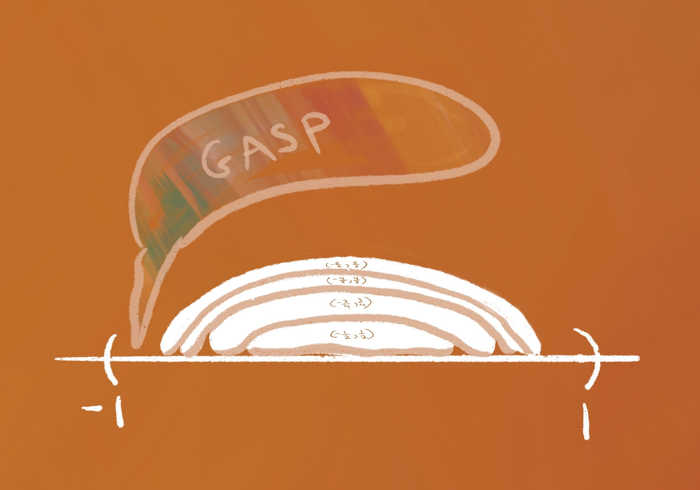
We know $\left\{ \left(-\frac{n}{n+1},\frac{n}{n+1} \right) : n \in \mathbb{N}\right\}$ covers $(-1,1)$.	Prove that no finite subset of it covers $(-1,1)$.

Scroll if you'd like a hint...

If you had a finite subcover $\mathcal{F}$, then it has a “largest pancake.” That is, there is a largest value of $n$ such that the pancake $\left( -\frac{n}{n+1},\frac{n}{n+1} \right)$ is in $\mathcal{F}$.

Scroll if you'd like to see the answer…

Suppose the largest pancake in $\mathcal{F}$ is $\left( -\frac{N}{N+1},\frac{N}{N+1} \right)$.

Then, the interval $\left[\frac{N}{N+1}, 1\right)$ is uncovered…so $\mathcal{F}$ can’t be a cover.